"The VC Investor’s Dilemma: Portfolio Construction Strategies for Every Distribution"
- ArtesianVC
- Aug 25, 2024
- 4 min read
In venture capital (VC), the power law distribution is commonly used to model returns because it reflects the reality that a few investments generate the majority of returns. However, other return distributions can also be considered to analyze risk and understand portfolio construction. Each distribution has different implications for how VCs might structure their portfolios. Here are some alternatives:
1. Normal (Gaussian) Distribution:
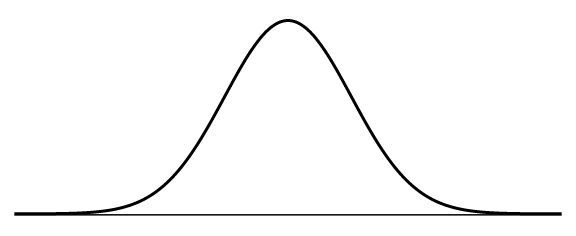
Characteristics:
Returns are symmetrically distributed around a mean, with most returns clustering around the average and extreme events (outliers) being very rare.
The tails of the distribution are thin, meaning extreme outcomes (both gains and losses) are very unlikely.
VC Portfolio Implications:
If VC returns followed a normal distribution, diversification wouldn’t be as critical because there would be fewer outliers.
Larger equity stakes in fewer companies might be prioritized, since the potential for extreme outsized winners would be lower, and the goal would be to capture consistent moderate returns from each investment.
The portfolio construction would focus on managing systematic risk (portfolio-wide risks) and minimizing downside by identifying consistent winners.
Conclusion: If VC returns followed a normal distribution, concentration on fewer, more certain bets would make sense. VCs would prioritize reducing risk and maximizing returns from more predictable, mid-level outcomes.
2. Lognormal Distribution:
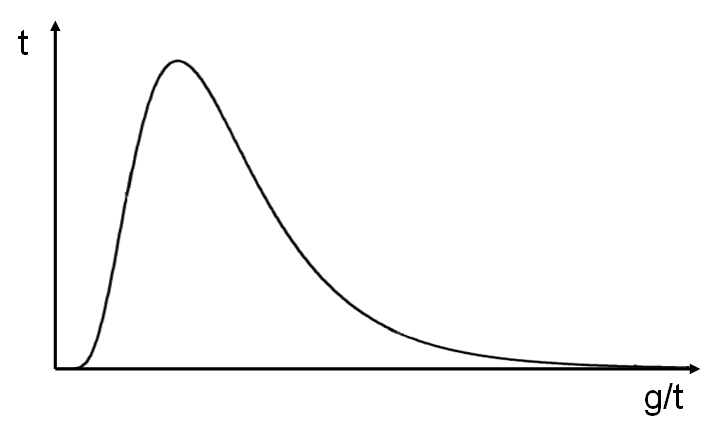
Characteristics:
A lognormal distribution is skewed, with most returns clustering around a lower value but a long right tail, meaning there’s potential for very high returns but most investments will result in smaller gains or losses.
Returns can't be negative (the distribution is bounded at zero) and there's a greater probability of small positive returns with rare large gains.
VC Portfolio Implications:
The long tail of the lognormal distribution suggests that some investments could generate very large returns, though not as frequently as under a power law.
Diversification is still important to capture those rare, large outcomes, but there might be more consistent positive returns across the portfolio.
VCs would still focus on capturing the upside potential of outliers but might place greater emphasis on managing downside risks as fewer total failures would be expected compared to a power law.
Conclusion: If VC returns followed a lognormal distribution, portfolio construction would still emphasize diversification to capture large winners, but VCs might expect more stable, smaller returns across the majority of the portfolio. They would focus on both mitigating losses and seeking outsized gains.
3. Exponential Distribution:
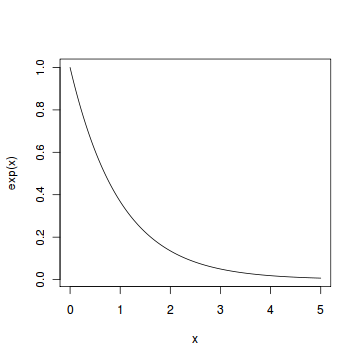
Characteristics:
The exponential distribution is heavily skewed, with a high probability of small returns and a smaller, decreasing probability of larger returns. There are no negative returns, and the risk of total loss might be lower than in a power law distribution.
The decline in probability for higher returns is faster than in a power law, meaning outliers are less likely.
VC Portfolio Implications:
Moderate diversification is important, but fewer extreme outliers exist compared to the power law distribution.
Smaller equity stakes across a moderate number of companies could be an effective strategy, as the distribution implies more companies will deliver positive, albeit smaller, returns.
Since very large outcomes are less likely, the focus would be on achieving consistent moderate returns across more investments.
Conclusion: If VC returns followed an exponential distribution, VCs would focus on balanced diversification—not too many investments, but enough to reduce risk. Emphasis would be on managing for consistent gains rather than aiming solely for unicorns.
4. Pareto Distribution (Power Law Variant):
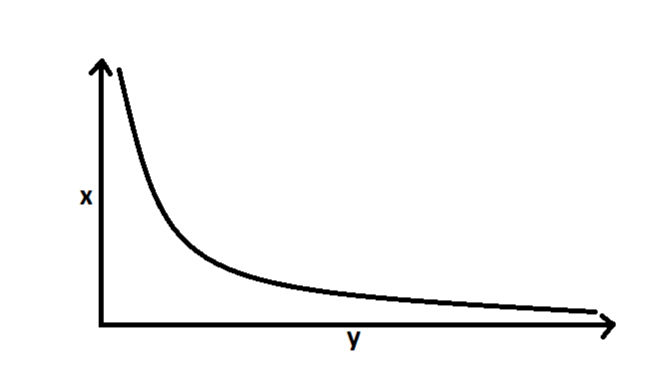
Characteristics:
Similar to a power law, the Pareto distribution has a "fat tail," where a small percentage of investments drive the majority of returns. This distribution emphasizes extreme outcomes more heavily than other distributions.
VC Portfolio Implications:
The Pareto principle (80/20 rule) applies, where 80% of returns come from 20% of the investments, meaning diversification is critical to ensure exposure to those few key winners.
Aggressive diversification is recommended, similar to the power law, as missing out on those rare outliers would disproportionately impact returns.
Follow-on investments in winners might also play a big role, as returns are likely concentrated in a very small number of companies.
Conclusion: With a Pareto distribution, VCs would again focus on broad diversification to ensure exposure to rare outliers. The portfolio would be structured around the expectation that most returns come from a few key investments, similar to a power law scenario.
5. Bernoulli Distribution (Binary Outcomes):
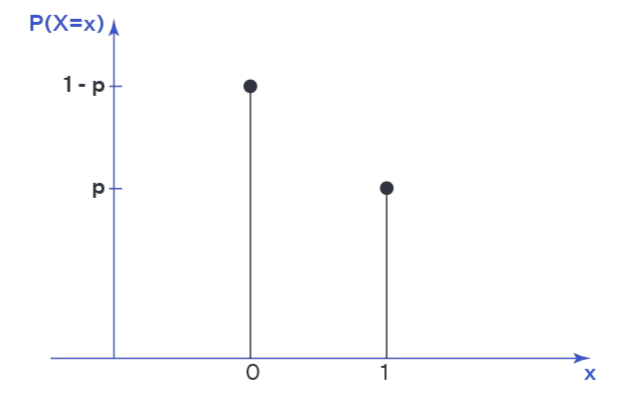
Characteristics:
The Bernoulli distribution has only two possible outcomes: success or failure. In a VC context, this could represent an investment either generating a significant return or failing completely.
This distribution doesn't account for the degree of success, only whether a company succeeds or fails.
VC Portfolio Implications:
High diversification would be necessary to spread the risk of binary outcomes. Since there’s no middle ground between success and failure, VCs would need to make enough bets to balance those that fail with those that succeed.
Equity stakes would become more important in companies that do succeed, but without more granular data on the size of returns, maximizing the number of investments would likely be the priority.
Conclusion: With a Bernoulli distribution, maximum diversification is critical to avoid over-reliance on any one investment. The portfolio would focus on spreading risk across many companies due to the high likelihood of failure.
Summary of Portfolio Implications for Each Distribution:
Power Law / Pareto: Aggressive diversification is essential. A few outliers will drive most returns, so VCs should invest in many startups to maximize chances of finding these outliers.
Lognormal: Diversification is still important, but there is a greater chance of consistent smaller returns. The focus is on capturing upside while managing downside risks.
Normal: Returns are more predictable, with fewer outliers. Concentration on fewer, high-quality investments with larger equity stakes might make sense, as extreme outcomes are less common.
Exponential: Some diversification is needed, but with a quicker decline in the probability of very large returns, the portfolio might emphasize moderate returns across a larger number of companies.
Bernoulli: Maximum diversification is key due to binary outcomes (success or failure). The focus is on reducing the risk of failure by spreading bets widely.





